[AES] 이론적인 접근으로
두비니
·2020. 4. 11. 13:22
AES
Advanced Encryption System
이론적으로 AES에 대해 다뤄보고자합니다. 다음글은 코딩적인 접근으로 해보자 합니다.
1. AES의 등장배경
원래는 DES라는 암호체계를 사용하고있었지만, $2^{56}$개의 키에대해서 전사적 공격이 가능해
취약한 알고리즘이 되었습니다.
(보통 $2^{60}$보다 작은 케이스로 전수조사가 가능하면, 그닥 안전하지 않은 알고리즘으로 분류합니다.)
물론 그 약점을 피하기위한 Triple DES같은 알고리즘이 많았지만,
효율적이지않아 결국 새로운 암호체계가 필요했습니다.
따라서 AES공모를 하게되었고, 다음과 같은 요구사항을 충족해야했습니다.
- 블록의 크기는 128비트
-대칭키 암호이며 세 종류의 키(128, 192, 256비트)를 사용할 수 있어야 함
-소프트웨어와 하드웨어 둘다 구현하기 효율적이여야함
-전수조사 이외의 현재 알려진 다른 암호 분석 공격에 강해야 함
- 전세계에서 무료로 사용 가능해야함
그래서 다음 5가지를 충족하는 암호가 지금 우리가 사용하는 AES입니다!
물론 이제는 양자컴퓨터의 개발에 따라 AES도 세대교체가 필요해지는 시점이 다가오고있기는 하지만,
현재는 최악의 경우 $2^{128}$번의 계산이 필요한, 안전한 알고리즘입니다.
간단한 역사는 이정도로 마무리하겠습니다.
2. AES 전체적인 구조
우선 AES의 간단한 소개 살펴봅시다.
-SPN구조
-한 블록: 128bit
-key(비밀): 128, 192, 256bit key
-10/12/14 라운드 수행
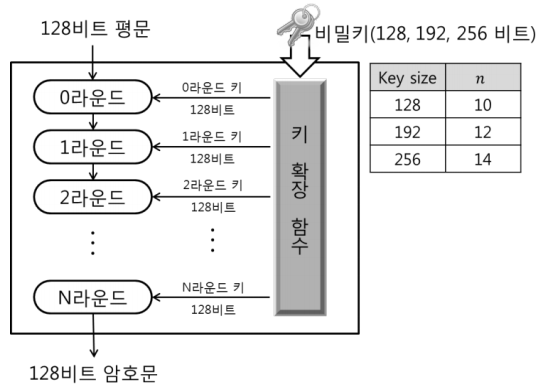
기본적으로 128bit의 평문이 입력되면, 128bit의 암호문이 나오게되는 구조입니다.
다만 이 평문을 암호화하는 비밀키는 128, 192, 256bit일수있는 것이구요.
암호화과정 횟수도 사용자의 설정에 따라 바뀝니다.
10라운드를 선택하면 0라운드부터 10라운드까지, 총 11번의 과정을 거친 후
최종 암호화가 됩니다. (라운드수는 횟수와 같지 않습니다)
이때 매 라운드때 라운드키가 필요합니다. 매 라운드마다 라운드키는 다르며,
라운드키는 키스케줄링이라는 과정을 통해 생성됩니다. 매 라운드마다 필요하기때문에 라운드키는 라운드가 총 N라운드일경우 N+1개가 필요하다는 것도 알 수 있네요.
다음으로 넘어가기전에 한가지만 더 설명을 하자면, AES상태(state)라는 게 있습니다.
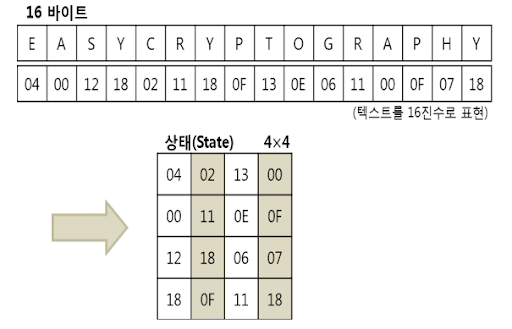
사진을 보면 쉬운데, 위와같이 16바이트(=128비트)가 주어진 상태에서,
우리는 다음과 같은 것을 4x4 행렬로 바꾼 뒤 계산을 진행합니다.
앞으로의 설명은 이걸 기본전제로 깔고가기때문에 알고계시면 좋을 것 같습니다!
다음은 AES의 구조입니다.
위에 라운드 얘기를 한 것이 기억이 나시나요?
만약에 12라운드를 택할시, 0~12라운드까지 총 13번의 연산과정을 거쳐 암호문을 만듭니다.
다음은 매 라운드에서 실행되는 과정의 설명입니다.
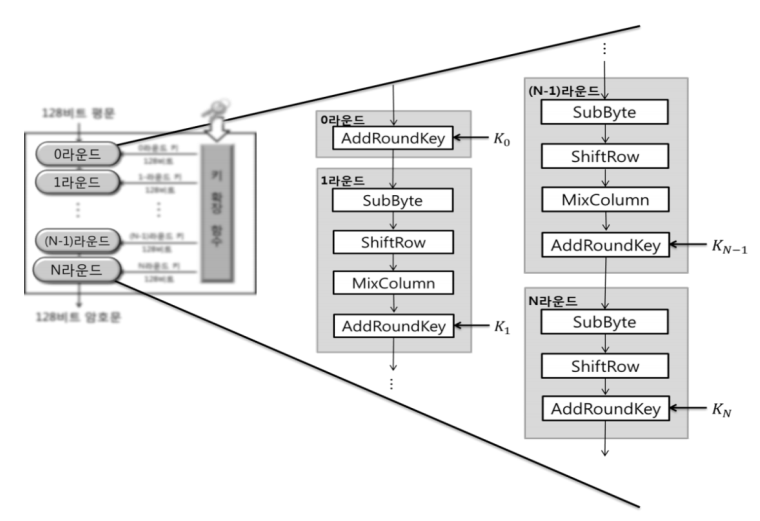
위 사진이 정말 사진 하나로 끝나는 AES입니다.
설명을 하자면 AES의 라운드들은, 과정을 기준으로 크게 3가지로 나눌 수 있습니다.
0라운드
1~N-1라운드
N라운드
로 나뉩니다. 사진을 봐도 조금씩 다른 것을 볼 수 있습니다.
각각의 단계들이 어떤 연산을 하는지는 밑에 더 자세히 다루도록 하겠습니다.
지금은 아 이런게 있구나 정도로만 하고 넘어갈게요.
우선 0라운드에서는 Addroundkey라는 과정만 거칩니다.
우선 여기서는 말그대로 RoundKey라는 비밀키를 더해주는, 즉 XOR해주는 과정을 거칩니다.
참고로 Addroundkey는 모든 라운드에서 실행됩니다.
1 ~ N-1 라운드에서는 모든 연산과정이 수행됩니다.
SubBytes >> ShiftRow >> MixColumn >> AddRoundKey
의 순서로 총 4개의 연산이 수행되고, 각 연산에 대한 설명은 뒤에 더 자세히 하겠습니다.
마지막으로 N라운드에서는 앞선 라운드에서 Mixcolumn을 제외해주면 됩니다.
그러면
SubByte >> ShiftRow >> AddRoundKey
의 과정이 되겠죠.
이런 과정으로 AES가 진행됩니다. 이제 각 함수들에 대해서 봅시다.
3. SubBytes
혹시 DES를 배우셨다면 S-box의 과정과 비슷한 과정입니다.
평문을 치환해주는 과정인데, 소프트웨어구현시에는 그냥 표를 이용합니다.
하지만 하드웨어로 구현시 이용하는 알고리즘이 따로 있습니다.
저도 공부할때 행렬연산때문에 애를 먹었는데, 아무튼 설명하겠습니다.

위 식이 SubBytes를 식으로 풀어쓴 과정입니다. Subbytes연산은 Affine Transformation과 inversion연산 과정을 거치게 되는데, 각 연산에 대해서 설명을 하도록 하겠습니다.
먼저 inversion과정입니다. AES의 SubBytes에서 이야기하는 inversion과정은 GF($2^8$)에서의 inversion의 연산을 뜻합니다. 여기에서 GF는 유한체를 말합니다. 여기까지 설명하면 글이 너무 길어지기 때문에 이걸 모르겠는 사람들은 따로 공부를 해봅시다ㅎ..
쉽게 이야기해서 그냥 기약다항식이 $x^{8}+x^{4}+x^{3}+x+1$인 상태로 Extended Euclidean Algorithm써서 역원구하는게 inversion과정 이라고합니다.
기약다항식을 $x^{8}+x^{4}+x^{3}+x+1$로 설정하는 이유는 8차 기약다항식 중, 항의 개수가 가장 적고, 감산이 쉬운 기약다항식이기 때문입니다.
왜 8차 기약다항식이냐구요? 8 bit = 1 byte...!
앗 Extended Euclidean Algorithm이 기억나지 않는다고요...?

혹시나 제 후배가 이걸 모르겠다면 자네는 암호수학을 열심히 듣지 않았군요.... 다시 공부합시다
아무튼 inversion과정을 통해서 $t^{-1}$을 구했다고 가정하고, Affine Transformation을 봅시다.


Affine Transformation은 행렬곱과 xor과정을 통해 진행됩니다.
저는 고등학교때 행렬을 배우지 않은 세대라 양껏 혼란스러워할 수 있었습니다.
아무튼, 왼쪽에 있는 저 A행렬은 상수값처럼 정해져있는 값이고, 저 $x_0$에서 $x_7$까지는 바꾸고자 하는 값을 넣으면 됩니다.
이때 주의할 점이, 값을 $x_7$에서부터 값을 거꾸로 넣어주여야 합니다.
예를 들어서 C6을 Affine Transformation을 해준다고 가정합시다.
그러면 C6을 이진수로 변환하면 11000110인데, $x_0$부터 1100...이렇게 들어가는게 아니라 $x_7$부터 1100...이런식으로 거꾸로 값을 넣어주어야합니다. 계산할때 저거때문에 고통받았던 기억이 아직도 생생하네요.
음 지금 이걸 보면서 무슨말인지 모르겠는데 대충 알고있으면 되는거 아닐까?라는 생각을 분명히 하고있을텐데,
뭐 이론만 알고 끝날거라면 상관없다만
나중에 직접 구현을 할거라면 정말 추천드리지 않습니다......왜 추천하지 않나구요? 저도 알고싶지 않았어요.....
아무튼 열심히 계산실수 내지않고 계산만 해주면 됩니다.
4. Shiftrow
다음은 Shiftrow과정입니다. 이건 말그대로 state상태에서 "shift", 즉 미는 과정입니다.
우선 state상태를 봅시다.
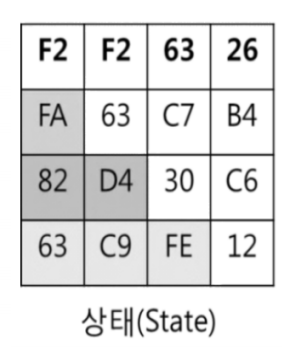
예를 들어서 다음과 같은 state가 있다고 생각합니다.
맨 윗줄부터 시작해서 차례로 0/1/2/3바이트를 왼쪽으로 돌립니다.
"돌린다"라는 말이 참 애매한데, 결과값을 보면 이해가 될겁니다.
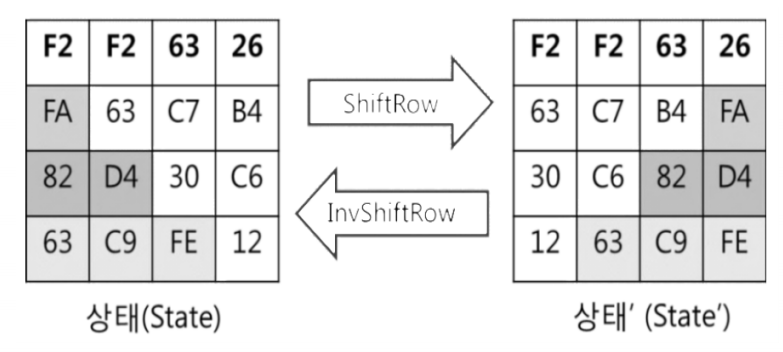
어떤 느낌인지 확 오죠? 그냥 단순히 이동하는거라 설명은 마무리하도록 하겠습니다.
5. MixColumn
다음은 MixColum입니다.
MixColumn같은 경우에는 단순한 행렬곱으로 진행됩니다. state상태에 있는 것들을 통째로 행렬곱을 하게 되고, 행렬곱을 하는 대상은 항상 정해져있습니다.

다음은 MixColumn과정을 간단하게 설명해놓은 건데, 간단하게 "아 그렇군"하고 넘어가도 되지만,
실제로 어떤식으로 계산하는지도 설명하도록 하겠습니다.
MixColumn도 SubBytes와 동일하게 GF($2^8$)에서의 곱셈 연산과 덧셈 연산을 이용해 계산합니다. 추가로 기약다항식이 $x^{8}+x^{4}+x^{3}+x+1$인 상태이기 때문에 곰셈도 다항식의 곱으로 풀어서 계산합니다.
예를 들어 곱셈 2 * 2C 를 계산한다고 합시다. 각각 2진수로 바꾼다면 10 * 00101100인데, 이를 다항식으로 생각한다면 10은 x로, 00101100은 $x^{5}+x^{3}+x^{2}$이므로 이 둘을 곱하면 $x^{6}+x^{4}+x^{3}$이고,
이를 다시 2진수/16진수로 바꾼다면 01011000/58이 됩니다.
굳이 이렇게 다항식으로 바꿔서 푸는 이유는 혹시라도 곱셈의 결과가 1바이트이상의 값을 가지는 경우 약분해주기 위함입니다.
6. AddRoundkey
마지막으로 Addroundkey입니다.
사실 이건 별로 설명할 것도 없어요.
그냥 KeySchedule로 만들어진 각각의 Roundkey를 Mixcolumn까지 진행된 state에 xor연산을 각각 해줍니다.

사실 여기에다가 keyschedule, 최적화, 그리고 복호화과정까지 써야하는데 생각보다 글이 너무 길어져서 여기서 한번 끊고 가겠습니다. 다음글에서 마저 설명하도록 하겠습니다!
+) 참고할만한 영상입니다. 깔끔하게 잘 정리되어있어서 올립니당
https://www.youtube.com/watch?v=gP4PqVGudtg
'Crypto' 카테고리의 다른 글
| Pollard's Rho에 대하여 (0) | 2020.09.09 |
|---|---|
| [LC] Toy Cipher Key Decryption code (0) | 2020.05.22 |
| [AES] Encryption Optimization code (0) | 2020.04.16 |
| [AES] AES_ENCRYPTION Code (0) | 2020.04.06 |
| Abstract (0) | 2020.02.06 |

