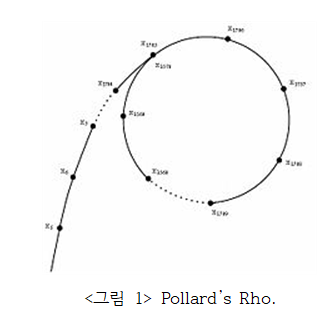
Pollard's Rho에 대하여
두비니
·2020. 9. 9. 02:29
Ⅰ. Pollard’s Rho에 대하여
Pollard’s Rho는 공개키 암호알고리즘에서 가장 많이 사용되는 계산 문제 중 하나인 인수분해 문제를 해결하기 위한 알고리즘 중 하나이다. Pollard’s Rho 알고리즘은 보통 10자리 이하의 수에 대한 수인수분해에 최적으로 알려져있는 알고리즘이다.
Pollard’s Rho에서 사용되는 이론은 다음과 같다.
1. 두 정수 x와 y는 다음과 같은 경우에 mod n에 대하여 합동이다.
1) 그들의 차가 n의 배수이다.
2) 각 숫자가 n으로 나누었을 때 같은 나머지를 갖는다.
2. GCD(Greatest Common Divisor), 즉 최대공약수는 각각 숫자들을 나누는 인수 중 가장 큰 숫자이다.
3. Birthday Paradox(생일 역설), 즉 두 사람이 같은 생일을 가질 확률은 적은 수의 사람(23명)만 있어도 매우 높다(50%).
4. Floyd’s cycle-finding algorithm: 거북이와 토끼가 원형 트랙에서 같이 시작하되, 토끼가 거북이의 2배로 달릴 경우 그 둘은 한 점에서 만날 수밖에 없다.
이 두 이론을 사용하게 된다. 이론을 간단히 설명하자면, 로 소인수의 개수가 2인 반소수(semi-prime) 또는 소인수의 개수가 3 이상인 카마이클 수(Carmichael number)인 합성수(composite number)라고 가정하자. 반소수 에서 의 배수는 개, 의 배수는 개, 로 개의 소인수 배수들 중에서 하나를 를 통해 찾는 것이다. 여기서 위에서 설명한 플로이드 순환 찾기 알고리즘을 같이 적용하면 두 수열이 동시에 순환하면서 1 또는 n의 약수를 찾아내기 때문에 이 원리를 이용하여 소인수를 찾아낸다.
위 그림과 같이 그리스 문자 를 닮았기 때문에 Pollard’s “Rho”라고 불린다. 이러한 Pollard’s Rho 알고리즘은 다음과 같다.
1. 무작위한 x와 c를 설정한다. y를 x와 동일하게 설정하고, 로 설정한다.
2. 약수를 찾지 못한 경우
1) x를 f(x)로 업데이트한다. (단, mod n)
이 과정은 Floyd’s cycle-finding algorithm에서 “tortoise move”를 하는 것과 같다.
2) y를 f(f(y))로 업데이트한다. (단, mod n)
이 과정은 Floyd’s cycle-finding algorithm에서 “hare move”를 하는 것과 같다.
3) |x-y|와 n의 최대공약수를 찾는다.
4) 최대공약수가 1이 아닌 다른 값일 경우:
(1) 최대공약수가 n인 경우, 새로운 x, y, 그리고 c값을 가지고 다시 모든 과정을 진행한다.
(2) 아니라면 그 최대공약수가 답이다.
이렇게 Pollard’s Rho가 진행된다. 이제 이를 기반으로 python code를 작성해보았다.
import math
import random
def PollardRho (n ):
if (n==1 ):
return 1
elif (n % 2 == 0 ):
return 2
#set x, y, and c
x = random.randint(0 , 2 )
y = x
c = random.randint(0 , 1 )
#d is cadidate divisor
d = 1
while (d==1 ):
x = (x**2 + c) % n #tortoise move
y = ((y**2 + c)**2 + c) %n
d = math.gcd(abs (x-y), n)
if (d==n):
return PollardRho(n)
return d
if __name__ == "__main__":
n = 10967535067
print ("One of the divisors for ", str (n), " is ", PollardRho(n))
다음은 예시로 작성한 코드이고, 결과는 다음과 같다.

정상적으로 잘 구해지는 걸 확인할 수 있다. 추가로 Pollard’s Rho의 시간복잡도는 로 의 시간복잡도를 가진 나눗셈시행법보다 훨씬 더 효율적인 것을 알 수 있다.
Ⅱ. Pollard’s Rho의 문제점
Pollard’s Rho는 확실히 나눗셈시행법이나 제곱합동법에 비해서 훨씬 빠르게 소인수를 찾을 수 있다는 장점이 있지만 특정 합성수에 대해서는 합성수를 찾지 못한다는 단점이 존재한다. 예를 들어 1027의 경우를 보자. 1027은 13과 79의 곱으로, 합성수이지만, 표1을 참고하면 Pollard’s Rho기법을 이용해서는 소인수를 찾아낼 수 없다는 것을 알 수 있다.

다음과 같이 소인수를 찾을 수 없는 경우, 초기값을 다시 설정해주어야 한다. 이러한 값들이 네자리수 안에서 총 15개가 발견된다. 즉, 에서 Pollard’s Rho 알고리즘의 오차율은 1.69%이다.
Ⅲ. Pollard’s Rho의 개선점
Pollard’s Rho에 다양한 개선점이 있지만, 가장 효율적인 다중 초기치 방법에 관해서만 서술하겠다. 기존의 Pollard’s Rho 알고리즘에서는 초기치를 로 초기화하여 알고리즘을 수행했다. 그러나, 1.69%의 반소수에 대해서는 소인수 분해 실패 확률을 가지고 있으며, 수행횟수도 번 수행된다. 이러한 소인수 분해 실패시 주어진 수 n이 합성수라면 의 값을 변경시키면서 다시 수행해야 한다.
이러한 문제점을 개선하기 위해 선행 논문[1]에서는 이 아닌 를 이용한다(단, ). 대신 기존 식인 는 변경되지 않으며, 초기치만 바꾼다.

실제로 다중 초기치 Pollard’s Rho를 적용시킨 결과, 앞서 기존의 Pollard’s Rho 알고리즘으로 구해낼 수 없었던 값들도 4번 이내로 소인수들을 찾아내었고, 추가로 Pollard’s Rho 알고리즘의 수행횟수 또한 67.94%를 감소시킬 수 있었음을 알 수 있다. 이외에도 다른 방법들이 있었지만, 다중 초기치 방법이 가장 수행횟수를 줄일 수 있었음을 시사한다.
Ⅳ. 결론
본 보고서에서는 Pollard’s Rho라는 알고리즘에 대해서 탐구해 보았다. Pollard’s Rho는 다른 소인수분해 알고리즘보다 탁월한 성능을 가지고 있다는 것을 알 수 있지만, 특정 합성수에 대해서는 소인수를 찾아내지 못한다는 단점과 이럴 경우 시간 손해가 심하다는 단점 또한 있었다. 이러한 단점을 해결하기 위해 다중 초기치 방법이 있다는 것을 알 수 있었으며, 다중 초기치 기법은 기존의 Pollard’s Rho가 분해하지 못했던 합성수들 뿐만아니라, 전반적으로 Pollard’s Rho 알고리즘의 수행횟수를 67.94% 감소시켰다는 점을 알 수 있었다.
===============
동아리에서 공부한 내용인데, 추후에 다중초기치 Pollard's Rho에 대해서 따로 구현해볼 계획이다.
'Crypto' 카테고리의 다른 글
| [RSA] RSA 공격법 (0) | 2020.09.27 |
|---|---|
| [RSA] 이론적인 접근으로 (0) | 2020.09.26 |
| [LC] Toy Cipher Key Decryption code (0) | 2020.05.22 |
| [AES] Encryption Optimization code (0) | 2020.04.16 |
| [AES] 이론적인 접근으로 (0) | 2020.04.11 |



