Finite Automata to Regular Expression : 두가지 방법으로
두비니
·2021. 4. 16. 22:30
Finite Automata to Regular Expression
두 가지 방법으로
이산수학이나 계산이론 등을 배우면, NFA를 DFA로, FA를 RE로 등등 형태변환이 항상 일어납니다. (제발 그만바꿔ㅠㅠ)
오늘은 FA를 RE로 바꾸는 과정을 알아볼건데, GNFA를 통해서 변환하거나, Arden's Rule을 활용하는 방법이 있습니다.
각 방법을 예시를 통해서 알아보도록 합시다. 고고
1. GNFA 이용하기
- GNFA 잠깐 소개
첫 번째 방법은 GNFA를 사용하는 방법입니다. GNFA에 대해서 모르신다구요????!!!
GNFA에 대하여
GNFA에 대하여 Generalized NFA 오늘은 GNFA입니다. (하루에 다 써올리고 있지만) 1. GNFA란 일단 GNFA는 Generalized Transition Graph(GTG)로도 불리우는 아이입니다. 기본적으로 GNFA는 Regular Expression의..
dokhakdubini.tistory.com
글 읽고 옵시다ㅎ
글 읽기 귀찮으시다면 GNFA의 조건만 기억하시면 됩니다.
| 1. GNFA로 만드려는 state들은 모두 accepting state와 starting state가 모두 아니여야함 2. GNFA는 NFA에서 중간에 존재하는 하나의 state를 줄여서 만들 수 있음(예시의 그림에서는 q제거) |
아무튼! 이걸 이용해서 NFA를 RE로 바꿔봅시다.
GNFA는 Regular Expression에서 사용하는 식을 transition으로 쓸 수 있기 때문에 식이 나올 때까지 변환하면 됩니다.
- 문제를 풉시다
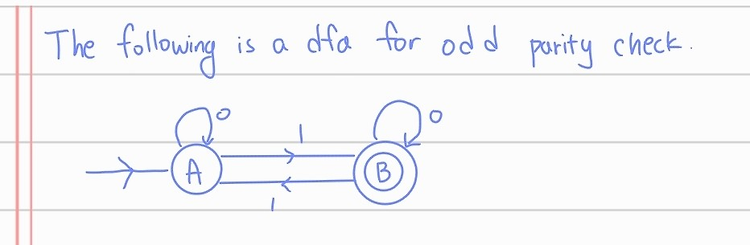
말로만 이야기 해서는 알기 힘들기때문에 같이 문제를 풀어봅시다.
예시로 다음 DFA를 RE로 바꿔봅시다. DFA보다 NFA가 더 큰 개념이기때문에 전혀 상관없죠?
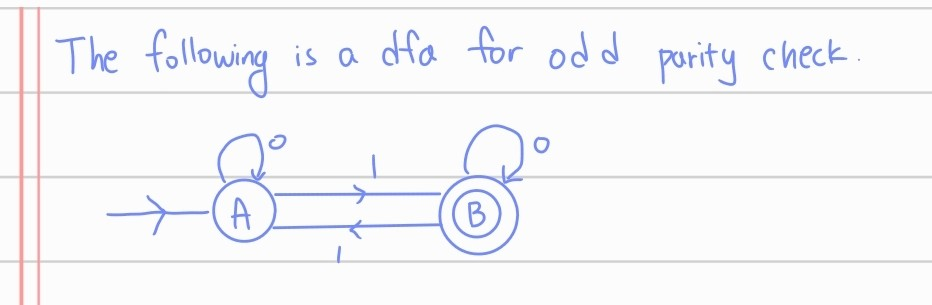
일단 GNFA의 조건을 맞추기 위해 DFA를 다음 NFA로 변경시킵니다.
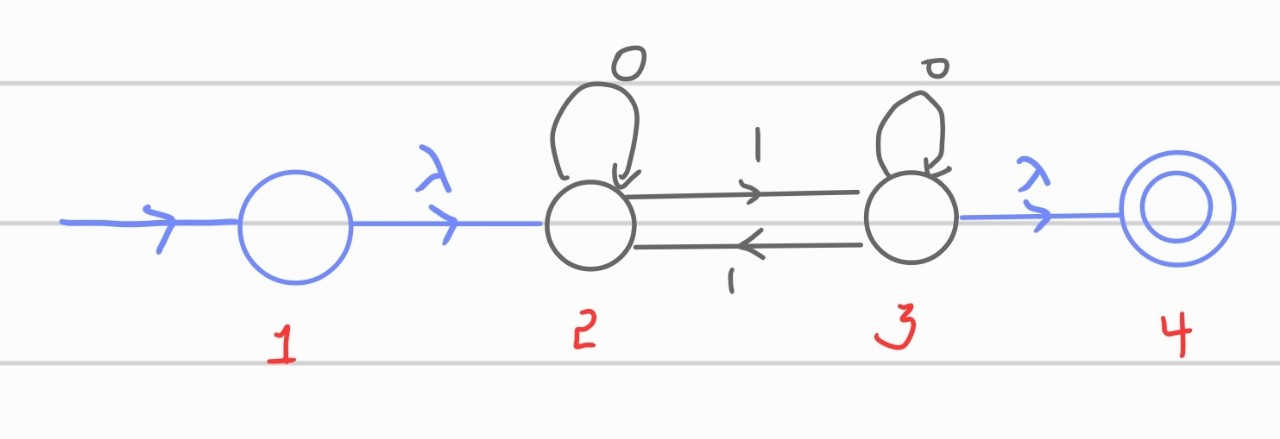
위처럼 굳이 바꾼 이유는 accepting state와 starting state가 모두 아니여야하기 때문입니다. 이 상태에서 두 가지 방법으로 풀이가 나뉩니다.
i) 1, 2, 3을 먼저 병합
ii) 2, 3, 4를 먼저 병합
이건 각 케이스를 모두 해보도록 하겠습니다.
i) 1, 2, 3을 먼저 병합
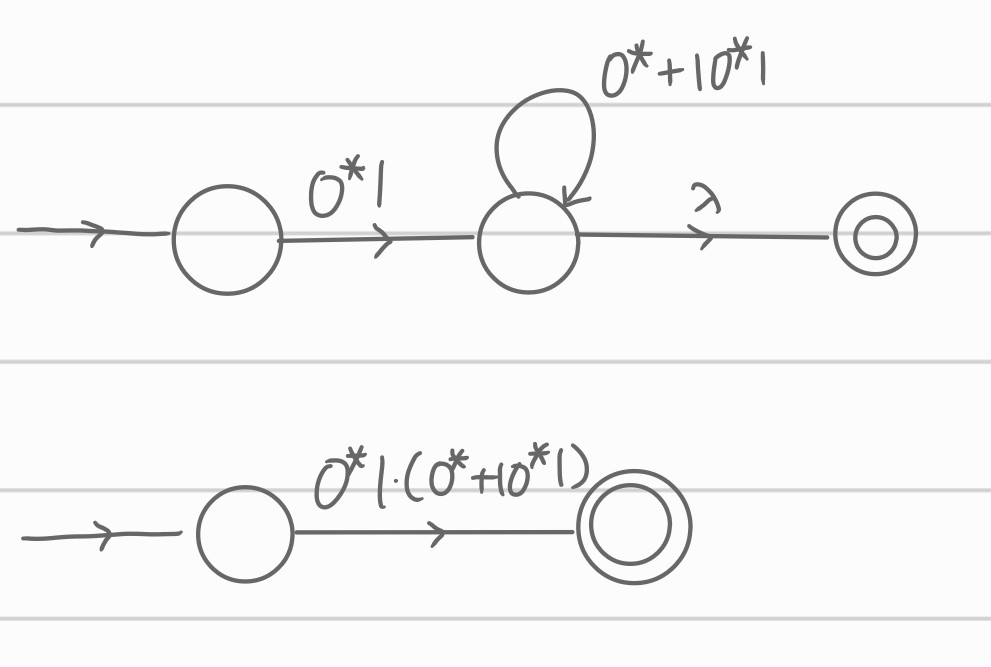
ii) 2, 3, 4를 먼저 병합
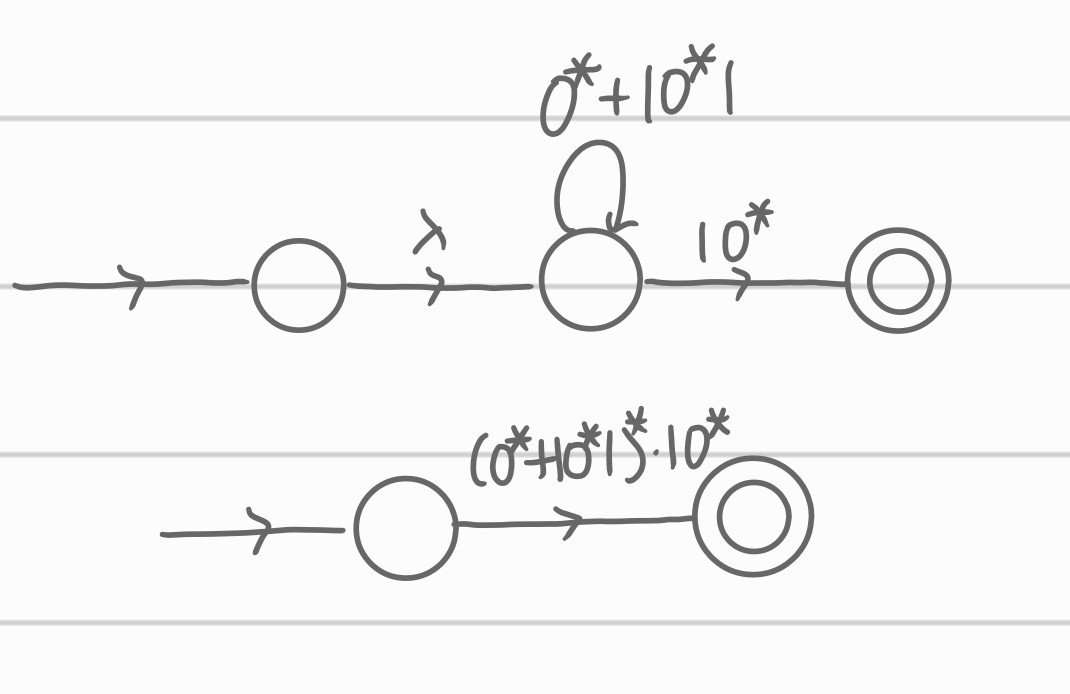
두 Regular Expression 모두 유효한 Expression들입니다. 중요한 점은 중복되지 않게 식을 표현하는 것입니다.
그럼 다음으로 갑시당
2. Arden's Rule 활용하기
두 번째 방법은 Arden's Rule입니다.
- Arden's Rule 잠깐 소개
Arden's Rule에 대해서 간단히 알아봅시다.
| Arden's rule states that the set A*⋅B is the smallest language that is a solution for the set X in the linear equation X = AX+B. i.e) X = AX + B, then X=A*⋅B X = XA + B, then X=B⋅A* |
결론적으로 밑에 써져있는 두 식만 쓸 줄 알면 됩니다.
Arden's Rule의 증명과정과 기본 지식을 알고싶다면 여기 : dokhakdubini.tistory.com/446
Arden's Rule에 대하여
Arden's Rule에 대하여 오늘은 Arden's Rule에 대해서 알아보고, 직접 증명할 예정입니다. Arden's Rule은 주로 DFA를 RE로 바꿀 때 주로 쓰인다고 합니다. 이 rule을 사용할 때 두 가지 표현방법이 있는데, 개
dokhakdubini.tistory.com
특히 위의 정의에서 i.e로 설명되어있는 두 식의 차이점을 모른다면 꼭 읽어보세여
- 문제를 풉시다

위와 같은 예시를 풀어봅시다.
i) outgoing
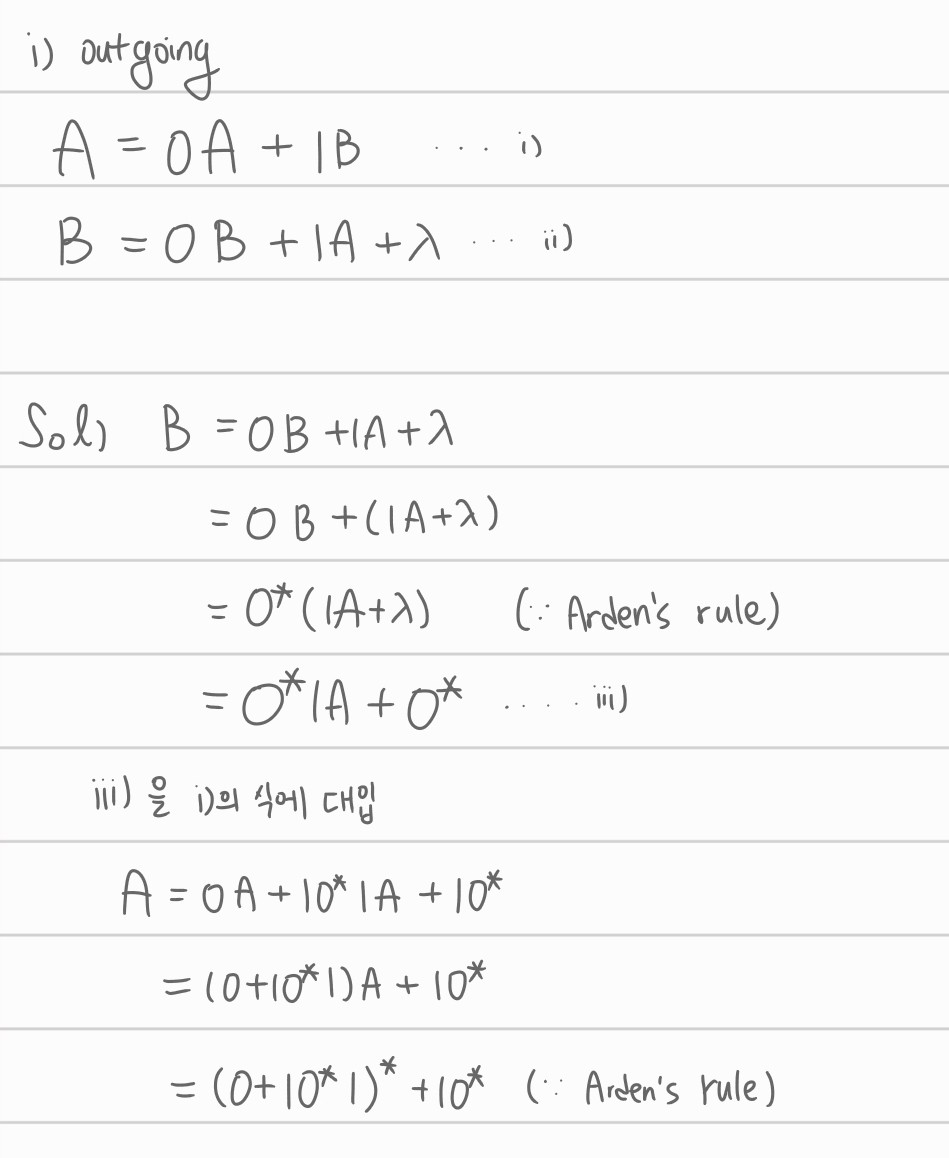
ii) incoming

그니깐 두 방법 모두 별건 아니고 어떻게든 arden's rule을 쓰기 위해서 정리를 해주면 되겠습니다.
만약 state가 3개 이상이면 대입을 통해서 변수를 2개로 정리한 뒤, 그 다음에 Arden's rule을 적용시켜주면 되겠죠?
그리고 결과를 보면 알 수 있겠지만 결국 GNFA를 통해서 얻어낸 결과와 같다는 것 또한 알 수 있습니다. 둘 다 결국 똑같다는거!
3. 결론
결론적으로 FA를 RE로 바꾸는 두 가지 방법에 대해서 알아봤습니다. 두 가지 방법중에 편한 걸 사용하면 될 것 같습니다.
개인적으로는 DFA는 Arden's Rule을 활용하고, NFA는 GNFA를 활용하는 쪽이 더 유리해 보이네요.
근데 시험을 치는 입장에서는 두가지 방법 모두 알아야겠져? 하..
암튼 우리모두 화이팅! 수학 ㅈ...조아!
'수학' 카테고리의 다른 글
| DFA 문제 팁 (0) | 2021.04.20 |
|---|---|
| DFA / NFA / Language 개념정리 (0) | 2021.04.20 |
| GNFA에 대하여 (0) | 2021.04.16 |
| Non-Finite Automata to Deterministic Finite Automata (0) | 2021.04.16 |
| Arden's Rule에 대하여 (0) | 2021.04.16 |




