DFA / NFA / Language 개념정리
두비니
·2021. 4. 20. 18:50
개념정리를 해봅시다
1. DFA (Deterministic finite Accepter/Automata)
dfa는 5개로 이루어진 튜플로 정의됩니다.
| M = (Q, ∑, 𝛿, q0 , F), where Q is a finite state of internal states, ∑ is a finite set of symbols called the input alphabet, 𝛿 : Q x ∑ → Q is a total function called the transition function, q0∈ Q is the initial state, F ⊆ Q is a set of final states. |
설명
1. Q는 존재하는 모든 state를 모아놓은 것입니다.
2. ∑는 transition으로 가능한 모든 문자들을 의미합니다. 그 화살표 위에 써져있는 친구들 말하는겁니다
3. 𝛿 는 transition function으로, 각 state에서 transition을 했을 때 어떤 state로 가게 되는지 알려주는 함수입니다.
4. q0는 intial state들입니다. 맨 처음에 화살표 받아서 시작하는 state요!
5. F는 final state들의 집합입니다.
예시
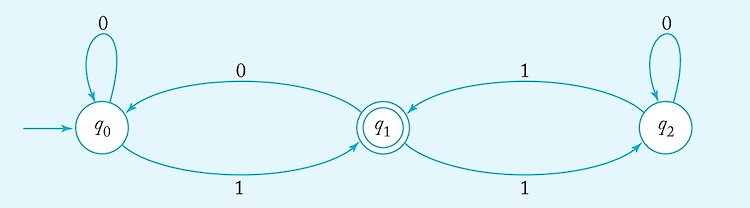
예시로 한번 봅시다

이걸 식으로 표현한다면 M = ({q0, q1, q2}, {0, 1}, 𝛿, q0, {q1}),
where 𝛿 is given by

* 이렇게 델타로 다 표현해도 되지만, 표로 표현해도 상관없다고 교수님께서 언급하심.
Final State F와 complement의 관계성
확통 유형 중 여집합의 경우를 구하고 그걸 전체 경우의 수에서 빼는 것처럼 여집합의 조건이 더 간단한 경우, DFA에서도 동일한 방법을 이용합니다.


다음은 M2와 M3의 두 가지 dfa를 그린 모습이다. 관찰해보면 두 dfa의 차이는 accepting state의 차이 빼고는 없는 것을 볼 수 있다. 그리고, 두 dfa를 받아들이는 조건의 경우 여집합의 관계이기 때문에, M2를 그린 후 M3을 그릴 때는 단순히 accepting state만 M2의 accepting state를 complement를 하면 된다.
참고로 이 방법은 accepting state가 여러개일 때도 성립한다.
이거 문제풀때 엄청많이 써먹음.
2. NFA(Non-Deterministic Finite Accepter/Automata)
nfa도 5개의 튜플로 이루어져있습니다.
| M = (Q, ∑, 𝛿, q0 , F), where Q is a finite state of internal states, ∑ is a finite set of symbols called the input alphabet, 𝛿 : Q x {∑∪{λ}} → 2Q is a total function called the transition function, q0∈ Q is the initial state, F ⊆ Q is a set of final states. |
다 똑같아서 다른 점만 보자면, 𝛿가 다릅니다.
말로 좀 풀어서 보자면, 우선 nfa는 람다연산이 가능하기 때문에 이게 추가되었다고 볼 수 있고, 이게 2Q가 되는 이유는 nfa가 multiple transitions를 가질 수 있기 때문에 Q의 부분집합에 속하는지 보는 것 뿐입니다.
NFA와 DFA의 차이점
우선 NFA는 DFA의 차이점만 보면 됩니다.
쉽게 얘기하면 NFA가 훨씬 더 제한이 없고, 그리는 입장에서 더 쉽습니다. 이동하지 않아도 쓸 수 있는 람다(λ)를 사용할 수 있고, 꼭 하나만의 transition을 가질 필요도 없습니다.
따라서 이걸 Nondeterminism이라고 하는데, 다음 두가지만 있다는 점을 알면 될 것 같습니다
- λ-transition
- Multiple transitions
Nondeterminism and Parallelism
그냥 당연한 말인거같은데, 대충 tree처럼 나뉘어지기 때문에 parallelism도 있다고 하는 것 같습니당
3-1. Language
기본적으로 language는 어떤 알파벳 ∑*의 부분집합입니다.
뒤에서 더 얘기하겠지만 그 부분집합이 특정한 규칙을 가지고 있다면 Regular Language이구요.
Language와 DFA의 관계성
기본적으로 Language라는게 특정 조건을 만족하는 string을 표현한 것이기 때문에, 그냥 automaton이 accept하는 string의 집합이라고 표현해도 됩니다.
그래서 DFA를 Language로 바꾸는 과정은 다음과 같습니다.
| The language accepted by a dfa M = (Q, ∑, 𝛿, q0 , F) is the set of all strings on ∑ accepted by M. In formal notation, L(M) = {w ∈ ∑* : 𝛿*(q0, w) ∈ F}. |
3-2. Regular Language
그리고 Regular Language라는 친구가 있는데, 얘는 위에서도 설명했듯이 Language들 중에서 특정한 규칙으로 표현할 수 있는 애들을 Regular Language라고 합니다.
그리고 dfa에 관련한 설명을 해야하는데, 위에서 이미 했기 때문에 넘어가도록 하겠습니다.
Calculation of Langage
언어 가 있다고 가정하고, 여러가지 연산을 해봅시다.
합집합 Union
두 언어 이 가지는 모든 문자열을 포함하는 연산입니다.
교집합 Intersection
두 언어 이 모두 가지는 문자열만을 포함하는 연산입니다.
여집합 Complementation
한 언어 의 알파벳으로 만들 수 있는 모든 문자열에서, 이 가지는 문자열을 제외한 모든 문자열을 포함하는 연산입니다.
접합 Concatenation
두 언어 이 가지는 모든 문자열을 결합 (concatenate) 하는 연산입니다.
반전 Reversal
한 언어 가 가지는 모든 문자열을 반전 (reverse) 처리한 언어입니다.
문자열의 길이가 모두 1이라, 반전처리해도 똑같은 회문임을 알 수 있습니다.
'수학' 카테고리의 다른 글
| Grammar의 정의와 Regular Grammar (0) | 2021.06.07 |
|---|---|
| DFA 문제 팁 (0) | 2021.04.20 |
| Finite Automata to Regular Expression : 두가지 방법으로 (0) | 2021.04.16 |
| GNFA에 대하여 (0) | 2021.04.16 |
| Non-Finite Automata to Deterministic Finite Automata (0) | 2021.04.16 |




