
Divide and Conquer 관점에서 본 Merge Sort
두비니
·2023. 6. 29. 04:05
Divide and Conquer 관점에서 본 Merge Sort
0. 개요
지난 글에 이어서 오늘은 Divide and Conquer approach에 대해서 알아보고, 나아가 Merge Sort에 대해서 알아보도록 하겠습니다.
1. Divide and Conquer
먼저 Divide and Conquer에 대해서 알아봅시다.

말 그대로 Divide(분할)한 뒤 Conquer(정복)하는 개념입니다.
가장 중요한 것은 Divide - Conquer - Combine의 순서로 진행된다는 점입니다.
이전 글이었던 Incremental approach와의 차이점에 대해서 이야기하자면, Incremental approach는 작게 문제를 나누어서 해결한 작은 문제를 기반으로 더 큰 문제를 풀어나간다면, 문제를 잘라놓고 모두 독립적으로 해결 한 뒤 마지막에 붙이는 느낌이라고 볼 수 있을 것 같습니다.
2. Merge Sort에 대해서
Merge Sort에 대한 정의를 알아봅시다.
합병 정렬 또는 병합 정렬(영어: merge sort 머지 소트)은 O(n log n) 비교 기반 정렬 알고리즘이다.
(Thank you Wikipedia)
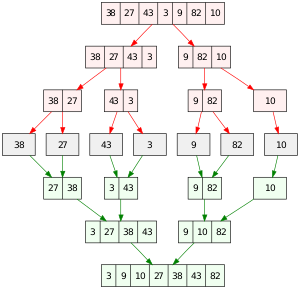
말 그대로, 배열을 계속해서 작게 자른 뒤 각 배열을 정렬하고, 배열을 합친 뒤 다시 정렬하는 형태로 진행된다.
이에 대한 의사코드는 다음과 같다.


3. 수행 시간 계산
수행 시간이 T(n)이라고 할 때, T(n)을 다음과 같이 정의하자.

설명을 덧붙이자면, c*n는 각 단계에서 merge 할 때 발생하는 시간을 뜻한다. 각 단계의 merge 시간이 c*n인 이유는 아래 그림을 보아도 잘 알 수 있다.

크기가 n인 subproblem에 대해서 merge할 때 발생하는 시간이 c*n이라고 가정하면, 이를 반으로 줄이는 경우 merge를 하는 시간 자체는 1/2로 줄어들겠지만, 전체 덩어리가 2개로 늘어났기 때문에 결국 결론은 c*n이다.
여기서 한 가지 더 궁금한 점은, n이 2보다 클 때 재귀함수의 형태로 작성되었다는 점이다. 결국 알고리즘에서는 선형적인 형태의 수식 및 답을 원하기 때문에, 딱 T(n)의 값을 구해보자.
그럼 위 tree의 높이가 l이라고 하자. 그렇다면 위에서 이야기한 T(n)은 l*n으로 나타낼 수 있다.
즉, 여기서는 l을 n에 대한 식으로만 표현할 수 있으면 T(n)을 구할 수 있는 것과 다름없다.
l을 구하는 과정은 간단하게 다음과 같이 표현할 수 있다.
| 1st Level | 1 |
| 2nd Level | 2 |
| 3rd Level | 4 = 2^2 |
| ... | ... |
| log(n)+1th Level | n = 2 ^ log(n) |
즉, 총 leaves의 개수가 n이 될 때는 log(n)-1층에 도달할 때다. 즉 l = log(n)+1임을 알 수 있고, 총 merge sort에 걸리는 시간은 c*n*log(n)+c*n임을 알 수 있다.
단, 시간 복잡도를 계산할 때는 상수항 및 계수를 고려하지 않기 때문에 T(n) = O(nlogn)이라는 결과 도출을 할 수 있다.
혹시 이 내용이 이해가 잘 안된다면 다음 글에 자세히 설명되어있다: https://ko.khanacademy.org/computing/computer-science/algorithms/merge-sort/a/analysis-of-merge-sort
병합 정렬 분석하기 (개념 이해하기) | 알고리즘 | Khan Academy
수학, 예술, 컴퓨터 프로그래밍, 경제, 물리학, 화학, 생물학, 의학, 금융, 역사 등을 무료로 학습해 보세요. 칸아카데미는 어디에서나 누구에게나 세계 최고의 무료 교육을 제공하는 미션을 가진
ko.khanacademy.org
'Coding_Algorithm > DS_Algorithm' 카테고리의 다른 글
| Probabilistic Analysis (0) | 2023.07.01 |
|---|---|
| Growth of Function (0) | 2023.06.30 |
| Incremental approach로 본 Insert sort algorithm (0) | 2023.06.28 |
| 알고리즘 & Halting Problem (0) | 2023.06.27 |
| [C로 쓴 자료구조론] 1장 연습문제-12번(멱급수) 풀이 (1) | 2020.05.17 |





