[RSA] 이론적인 접근으로
두비니
·2020. 9. 26. 20:30
RSA
이론적인 접근으로
이번에 다뤄볼 암호체계는 RSA입니다.
0. 배경지식-공개키 암호 시스템
RSA 알고리즘을 이해하기 위해서 기본적으로 공개키 암호 시스템에 대해서 가볍게나마 훑어보겠습니다.
읽어보고 아직 잘 모르겠다 싶은 부분이 있다면 따로 더 공부를 한 뒤에 읽는걸 추천드립니다.
= 공개키 암호 시스템 =
비대칭키 암호 시스템이라고도 합니다. 개인적으로 비대칭키 암호 시스템이라고 알고있는 것이 직관적인 이해를 돕는 것 같습니다.
암호화, 복호화에 사용되는 키가 서로 다른 암호 시스템이고, 암호화키를 공개합니다. (왜 공개키 암호/비대칭키 암호인지 알겠죠?)
대칭키 암호화 비교했을 때 엄청나게 많은 연산량을 필요로 하기 때문에 보통 키 분배 문제 해결을 위해 사용됩니다.
더불어 많은 연산량 덕분에 매우매우 느립니다.
일단 이것만 봐서는 어떻게 암호화 및 복호화를 할 수 있는지 궁금할텐데, 기본 아이디어는 다음과 같습니다.
0. A가 자신만 알고 있는 기밀을 B에게 전달하려고 합니다.
1. B가 자신의 공개키를 공개합니다.
2. A는 B가 공개한 공개키를 가지고 문서를 암호화합니다.
3. 암호화된 문서를 B에게 전달합니다.
4. B는 자신이 가진 개인키로 이 문서를 해독해봅니다.
그니깐 쉽게 이야기해서 자물쇠와 키 중 자물쇠만 B가 공개하고, A는 자물쇠로 잠궈서 내용을 보내주면 B가 열어보는 식입니다.
이런 방법을 사용할 경우, 타인이 전달과정에서 암호화된 문서를 가로채더라도 B의 개인키가 없다면 해독을 할 수 없습니다.
이 내용이 실전에서는 다음과 같이 응용되어 쓰일 수 있습니다.
- 기밀내용의 전달
- 발행자의 증명
-문서 변조 방지
더 많은 내용은 여기! : wiki.hash.kr/index.php/%EB%B9%84%EB%8C%80%EC%B9%AD%ED%82%A4
1. RSA 암호 알고리즘이란?
RSA 알고리즘이란, 미국 MIT에서 개발한 공개키 암호 시스템으로, 현재 전자상거래(SSL/TLS)에서 가장 흔히 쓰이고 있는 알고리즘입니다.
이 알고리즘은 소인수분해 문제에 기반하고 있습니다.
소인수분해 문제란, 3개의 큰 소수 p, q와 두 값의 곱 n에 대해서 n을 알고있어도 p와 q를 알아내기 어렵다는 문제입니다.
1977년 이 알고리즘을 개발한 Ron Rivest, Adi Shamir, Leonard Adleman 이 세 사람의 성을 따서 RSA라고 이름을 붙였습니다.
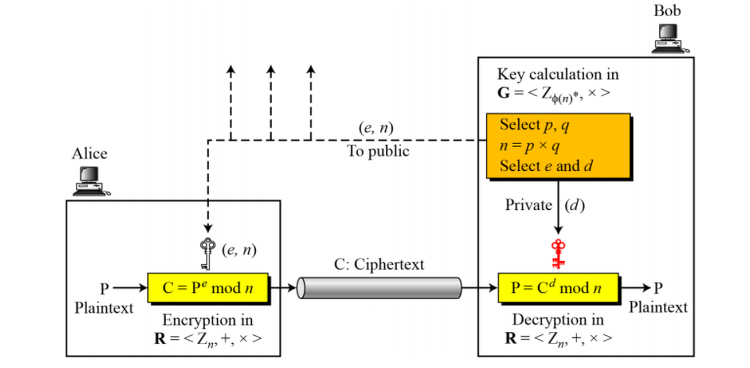
2. RSA의 전체적인 구조
다음은 RSA 알고리즘의 큰 틀입니다.

RSA는 크게 키 생성 - 키 분배 - 암호화 - 복호화 의 단계를 거칩니다.
예시를 통해 설명하도록 하겠습니다.
전체적인 과정은 위에 설명해놓은 공개키의 진행 과정과 같습니다.
이제 각 단계에 대해서 알아봅시다.
각 단계를 Alice와 Bob을 기준으로 작성하도록 하겠습니다.
3. 키 생성
키 생성은 공개키와 개인키를 만들어야 합니다.
키를 만들기 위해서 p, q, n, e, d 총 5개의 변수가 사용됩니다. 아래는 각각을 설명하는 내용입니다.
- n 구하기
임의의 두 소수 p와 q를 정한 뒤, n = p* q로 n을 구한다.
-e 구하기
우선 Φ(n) = (p - 1) * (q - 1)을 이용하여 Φ(n)을 구한다.
이때 e는 1 < e < Φ(n)를 만족하는 Φ(n)과 서로소인 수를 e로 설정한다.
참고로 e는 보통 65537로 설정합니다.
-d 구하기
d는 다음 식을 만족하는 값을 d로 설정한다.
(e * d) mod Φ(n) = 1
즉 e*d를 Φ(n)를 나누었을 때 나머지가 1인 d를 구하면 된다.
이렇게 구한 값들은
공개키 : (n, e)
개인키 : (n, d)
로 사용된다. 어떻게 사용되는지는 암호화를 봅시다.
4. 암호화
암호화식은 다음과 같습니다.
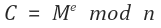
M은 평문, C는 암호문에 해당합니다.
이렇게 암호화를 Alice가 공개키 (n, e)를 통해 암호화를 진행합니다.
5. 복호화
그렇게 Alice가 암호화한 값을 Bob이 받고, 이를 다음과 같은 식으로 해독합니다.

식이 성립하는 이유는 페르마의 소정리 때문이며, 조금 풀어쓰자면 다음과 같습니다.

이렇게 Alice는 Bob에게 안전하게 정보를 전달할 수 있게 됩니다.
생각보다 많이 간단하게 정리되네요. 다음 글에서는 공격법에 대해서 써보도록 하겠습니다.
'Crypto' 카테고리의 다른 글
| Weiner's Attack cheat sheet (0) | 2021.05.15 |
|---|---|
| [RSA] RSA 공격법 (0) | 2020.09.27 |
| Pollard's Rho에 대하여 (0) | 2020.09.09 |
| [LC] Toy Cipher Key Decryption code (0) | 2020.05.22 |
| [AES] Encryption Optimization code (0) | 2020.04.16 |



