[RSA] RSA 공격법
두비니
·2020. 9. 27. 08:10
RSA 공격법
CTF에서 크립토문제로 생각보다 자주 출제되는 RSA 이다.
크게 분류하면 적절하지 못한 소수를 택한 경우 / 구조상 문제로 나뉜다.
0. 개인키 유출
p, q, ϕ(n), d 중 단 하나라도 노출된다면 나머지 키들을 모두 획득할 수 있다.
방법은 확장된 유클리드 호제법을 사용하면 간단하게 구할 수 있다.
이론은 이전글 참고 : dokhakdubini.tistory.com/288
[RSA] 이론적인 접근으로
RSA 이론적인 접근으로 이번에 다뤄볼 암호체계는 RSA입니다. 0. 배경지식-공개키 암호 시스템 RSA 알고리즘을 이해하기 위해서 기본적으로 공개키 암호 시스템에 대해서 가볍게나마 훑어보겠습니
dokhakdubini.tistory.com
1. 소인수분해
n을 소인수분해 할 수 있다면 개인키가 유출된 것이나 다름없다.
이론적으로 계산량을 줄여줄 수 있는 알고리즘은 다음과 같다.
각각 설명하기에는 글이 너무 길어지기에 링크를 첨부한다.
pollard-(p-1) Algorithm : www.geeksforgeeks.org/pollard-p-1-algorithm/
pollard's rho Algorithm : dokhakdubini.tistory.com/257?category=832455
Dixon's Random Square Algorithm : cs.indstate.edu/~nyellu/Dixons.pdf
그리고 일단 실전에 쓸 수 있는 DB들도 있다:
FatorDB : http://factordb.com/
ECM : https://www.alpertron.com.ar/ECM.HTM
2. 선택 암호문 공격(Chosen Ciphertext Attack)
우선 선택 암호문 공격은 임의로 선택된 암호문과 일치하는 평문으로부터 암호키를 알아내기 위해 시도하는 공격이다.
즉 원하는 암호문을 복호화해주는 경우 사용할 수 있는 공격 방법이다.
RSA에서 쓰이는 경우는 "곱셈에 대한 준동형사상(Homomorphism)의 성질"이라고 한다.
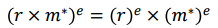
곱셈에 대한 준동형사상은 다음 식으로 정리될 수 있으며, 이를 이용하면 다음과 같은 공격이 가능해진다.
예시를 들어보자.
암호화된 flag가 있고, 암/복호화 기능이 존재한다고 가정하자.
그럼 푸는 방법은 다음과 같다.
1. 숫자 2를 암호화 한다.
2. 수사 2를 암호화 한 값과 flag를 암호화 한 값을 곱한다.
3. 결과 값을 숫자 2로 나누면 flag가 된다.
덧붙여, 이 방법을 막기 위해서 고안된 방법은 RSA-OAEP를 제안하였다.
RSA-OAEP는 암호화 단계에서 평문 해시값과 정해진 개수의 '0' 등으로 만들어진 "인증 정보"를 평문의 앞에 추가하고 RSA로 암호화한다.
이후 복호화단계에서 이 "인증 정보"가 보이지 않을 경우 평문을 알고 있는 사람이 만든 암호문이 아니라고 판단하여 복호화를 진행하지 않는다.
실제로 RSA-OAEP에서는 난수를 이용하는 등 암호문이 매번 다른 패턴이 되도록 하여 안전성을 높였다.
3. 낮은 지수 공격(Cycling Attack)
이 공격은 e값이 매우 작고, n값이 큰 경우 가능하다.
컴퓨터 모듈러 연산의 속도를 위하여 e값으로 페르마 소수 F0, F2, F4를 사용하는 경우가 많다.
e값이 매우 작고, n값이 큰 경우 암호문 C아 모듈러 연산에 걸리지 않는 경우가 있다.
이 경우에는 그냥 e 거듭제곱근을 구해서 평문을 복호화해 낼 수가 있다.
python에서 지원해주는 gmpy모듈을 이용할 수 있다.
c, e값이 주어졌고, 그 중 e가 3이라고 가정하자.
from gmpy2 import *
c =
with local_context() as ctx:
ctx.precision = 3000
m = cbrt(c)
#m = iroot(c, 3)[0]
print ('%x' % int(m)).decode("hex")
그럼 다음과 같이 공격할 수 있게 된다.
4. Fermat factorization 공격
소수 중 페르마소수(Fermat number)라는 값들이 있다.
이러한 값들을 사용하게 되는 경우 소인수분해가 매우 쉬워지게 된다.
과정은 다음과 같다
: 접근 :
- n = pq 가 두 양수의 곱이라면, n은 홀수이기 때문에 p와 q 모두 홀수이다.
- a = 1/2 * (p+q) and b = 1/2 * (q-p)라고 가정하자.
- a와 b는 모두 정수이기 때문에, p = (a – b) and q = (a + b)이다.
- 즉, n = pq = (a – b)(a + b) = a^2 – b^2이다.
- n이 소수인 경우, b = 1이 될때까지 1번으로 돌아가 진행한다.
+) 참고 : blog.naver.com/mouse0333/221319808610
위 라업의 첫번째 방법이 fermat factorization을 이용하였다.
5. Weiner's Attack 공격
이 공격은 e값이 매우 큰 경우 이 공격을 사용할 수 있다.
원리는 다음과 같다.
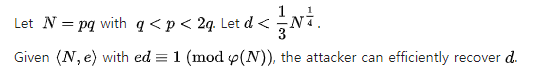
기본적으로 e값이 큰 경우 d값이 작을 확률이 더 높고, 이를 이용하여 공격할 수 있다.
이 공격에 대해서 이미 python으로 구현된 부분이 있어서, 해당 링크를 첨부한다 : github.com/pablocelayes/rsa-wiener-attack
pablocelayes/rsa-wiener-attack
A Python implementation of the Wiener attack on RSA public-key encryption scheme. - pablocelayes/rsa-wiener-attack
github.com
6. 하스타드 공격
1. e=3, {n1, n2, n3}에 대해 동일한 평문 M을 3개 전송하였을 때
2. c1, c2, c3가 존재한다. (각각 (n1,e), (n2,e), (n3,e)로 암호화)
3. 중국인의 나머지정리(CRT)를 이용하여 c^t == x (mod n1n2n3)를 계산
4. m^3 < n1n2n3 이기 때문에 c^t=m^3
이를 이용하여 공격할 수 있다.
aaossa/Computer-Security-Algorithms
Problems related to computer security. Algorithms written in Python. Learn more: https://id0-rsa.pub/ - aaossa/Computer-Security-Algorithms
github.com
::참고링크::
'Crypto' 카테고리의 다른 글
| base64 encoding 알아보기 (좀 필요 이상으로 많이) (0) | 2021.07.07 |
|---|---|
| Weiner's Attack cheat sheet (0) | 2021.05.15 |
| [RSA] 이론적인 접근으로 (0) | 2020.09.26 |
| Pollard's Rho에 대하여 (0) | 2020.09.09 |
| [LC] Toy Cipher Key Decryption code (0) | 2020.05.22 |




