공개키 암호에 대한 이모저모 (1) - based on 소인수분해
두비니
·2021. 7. 8. 17:39
공개키 암호에 대한 이모저모 (1)
RSA, Rabin
이번에는 공개키 암호화에 대해서 몇 가지 알아봅시다.
시험공부를 위한 암기만 했더니 다시 보니깐 이름만 어디서 본 거같고 아무고토 알 수 없습니다...
너무 깊게까지는 안들어가고, 전반적으로 무엇인지 알 수 있을 정도로만 정리하도록 하겠습니다.
0. 공개키 암호
정말정말 간단하게 설명하고 넘어갈게요. 공개키암호 보다는 비대칭키 암호라는 단어를 더 좋아해서, 이걸로 설명하겠습니다.
비대칭키, 즉 암호화/복호화를 하는 키는 2개이며, 하나는 공개, 하나는 비공개로 하여 암호화/복호화하는 과정입니다.
이 키들을 각각 공개/비공개키라고 합니다.
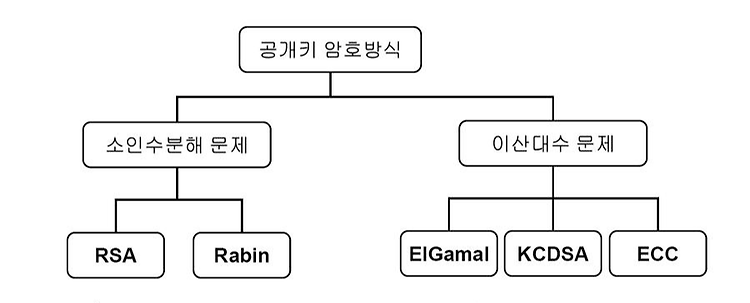
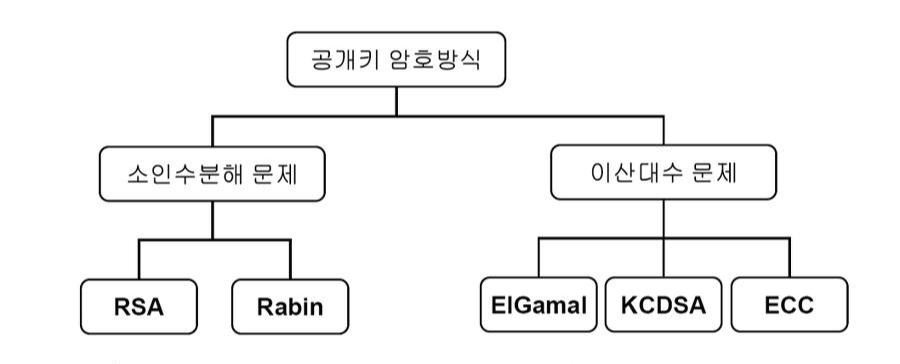
일단 각 키는 보통 수학적 문제에 기반하여 생성합니다. 그래서 키의 생성 과정은 비공개키를 통해 공개키를 만들어 내지만, 이러한 수학적 문제때문에 공개키를 기반으로 비공개키를 알아낼 수는 없습니다. 이건 소인수분해 문제와 이산대수 문제로 나뉘구요. 두 카테고리에 따라 오늘 이야기할 5가지 암호화 알고리즘이 나옵니다.
가장 쉽게 이해 할 수 있는 예시는 우체통으로 이해할 수 있을 것 같습니다. 우체통이 있다고 했을 때, 일반인들은 그 우체통 안에 편지를 넣을수만 있다고 가정합시다. 대신, 우체통의 주인은 열쇠를 통해 우체통을 열 수 있는 것이죠. 그렇다면 이 우체통의 위치는 공개키 암호화 과정에서 공개키가 되는 것이고, 주인이 가지고 있는 열쇠가 비공개키, 즉 개인키가 되는 것입니다.
2. 소인수분해 문제
자 그러면 이 공개키의 핵심은 "어떻게 공개키/개인키를 생성할 것인가?"입니다.
가장 대표적인 예시인 RSA와 Rabin암호가 포함되어있는 소인수분해 문제에 대해서 먼저 알아봅시다.
소인수분해 문제는 쉽게 말해 다음과 같습니다.
어떤 엄청나게 큰 소수 p, q가 있을 때, 둘을 곱한 값 n만 알고있다면 소인수분해가 불가능하지 않을까? 라는 생각에서 나옵니다.
사실 이걸 논하기 전에 많은 것들을 증명해야합니다. 소수의 갯수는 무한하다던가, 인수를 구하기 위해서 시도해야하는 횟수라던가 등등 몇가지를 해야하지만, 앞서 말했듯 수박겉핥기만 할거기 때문에 결론만 말씀드릴게요.
개 어렵습니다... 단순히 생각해봅시다. 그냥 우리가 손으로 뭐 한 20자리 숫자와 200자리 숫자를 인수분해한다고 하면,
당연히 200따리 숫자를 인수분해 하는데 더 애를 먹겠죠?? 이걸 컴퓨터의 입장으로도 풀지 못하게 하여 이용하는 것이 쇤수분해 문제를 활용한 공개키 암호화입니다.
1) RSA
열심히 적고있었는데 대박! 과거의 내가 글을 작성한 적이 있네요. 과거의 나 사랑해
https://dokhakdubini.tistory.com/288
[RSA] 이론적인 접근으로
RSA 이론적인 접근으로 이번에 다뤄볼 암호체계는 RSA입니다. 0. 배경지식-공개키 암호 시스템 RSA 알고리즘을 이해하기 위해서 기본적으로 공개키 암호 시스템에 대해서 가볍게나마 훑어보겠습니
dokhakdubini.tistory.com
2) Rabin암호
Rabin암호는 기본적으로 RSA와 같은 원리이지만, 더 간단하다고 볼 수 있습니다.
한줄정리하자면 RSA시스템에서 e와 d의 값을 2로 고정시키는 경우입니다.
덕분에 더 빠르게 계산한다는 장점 또한 있습니다.
과정은 진짜 단순해서 위키로 대신합니다. https://ko.wikipedia.org/wiki/%EB%9D%BC%EB%B9%88_%EC%95%94%ED%98%B8%EC%B2%B4%EA%B3%84
라빈 암호체계 - 위키백과, 우리 모두의 백과사전
라빈 암호(Rabin cryptosystem)는 미하엘 라빈이 1979년1월에 발표한, 소인수분해 기반 공개키 암호(비대칭 암호)이다. 공개키로 암호화하고, 개인키로 복호화한다. 중국인의 나머지정리(Chinese Remainder T
ko.wikipedia.org
일단 끝!
다음글로 공개키 마무리하도록 하겠습니다.
'Crypto' 카테고리의 다른 글
| Rainbow Table Attack 알아보기 (0) | 2023.01.03 |
|---|---|
| Hashcat 사용기 (0) | 2022.12.20 |
| base64 encoding 알아보기 (좀 필요 이상으로 많이) (0) | 2021.07.07 |
| Weiner's Attack cheat sheet (0) | 2021.05.15 |
| [RSA] RSA 공격법 (0) | 2020.09.27 |




